5 min read Reinforcement Learning

Advantage Actor Critic (A2C)

Advantage Actor Critic (A2C)
Photo by GR Stocks / Unsplash

It seems we've overlooked an important method in policy-based approaches: the Actor-Critic algorithm. In fact, we've already discussed a more advanced variant built upon it— Soft Actor Critic (SAC) and Proximal Policy Optimization (PPO) . However, to truly understand the intricate components of such algorithms—and to gain the ability to improve or develop new ones—it's essential to have a solid grasp of the foundational concepts.

Actor Critic Introduction

In brief, the Actor-Critic algorithm is a hybrid approach that combines policy-based methods (via the Actor network) and value-based methods (via the Critic network) to optimize an agent's decision-making process. Below, we outline its core components:

  1. Policy (Actor)
    • A probability distribution over actions given states by 𝜽, denoted as $π_{θ}$
    • Adjust 𝜽 to increase the likelihood of actions that lead to higher rewards
  2. Value Function (Critic)
    • Estimates the expected reward with the value function $V(s;w)$ or $Q(s,a;w)$
    • Evaluates the choosen action
  3. Advantage Function
    • Critic network computes the advantage function, which measures how much better an action is compared to the average action in state $A(s, a) = Q(s, a) - V(s)$, often approximated with $A(s,a) \approx r + γV(s';w) - V(s;w)$
      • A > 0: increase probability of action a
      • A < 0: decrease probability of action a

The full procedure of the algorithm is followed:

  1. Initialization: initialize θ and 𝑤 for actor and critic networks

  2. Interaction: observe state $s$ and sample action $a \sim π(a|s;θ)$

  3. Critic Update:

    • Compute the TD error to update the critic: $\delta = r + γV(s';w) - V(s,w)$
    • Update $w$ to minimize the TD error $w \leftarrow w + ⍺\delta∇_w V(s;w)$

  4. Actor Update:

    • Update the actor policy to favor actions with positive advantage $θ \leftarrow θ + ⍺\delta∇θ \log{π(a|s;θ)}$ and $∇{θ}J(θ) \approx 𝔼[\delta ∇_{θ}\log{π(a|s;θ)}]$
    • $\delta > 0 \rightarrow \text{increase} \space π(a|s;θ) $
    • $\delta < 0 \rightarrow \text{decrease} \space π(a|s;θ) $

We can tell from the procedure that Actor-Critic are actually policy improvement and evaluation respectively.

Pros and Cons

  1. Pros
    • Hybrid Approach: combines the strength of policy-based and value-based
    • Flexibility: works in both discrete and continuous action spaces
    • Online Learning: learn incrementally, suitable for real-time applications
  2. Cons
    • Convergence: not guaranteed to converge to the global optimum
    • Bias: may introduce bias if poorly approximated

Many RL algorithms are built upon the Actor-Critic framework, including those we've already introduced, such as PPO and SAC. However, there are several other notable variants worth discussing in the future, such as A2C, A3C, and DDPG.

Actor Critic Implementation

We use the Pendulum-v1 environment to explore the inner workings of the Actor-Critic algorithm. In this section, we focus on describing the network architecture and how it interacts with the environment. Additionally, to stabilize training, I have applied some normalization techniques, which you can find implemented in the codebase.

Actor Network

class Actor(nn.Module):
    """Actor network that outputs action parameters for continuous action space"""

    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(Actor, self).__init__()

        self.actor_net = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, action_dim),
            nn.Tanh()
        )

        self.log_std = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        mean = self.actor_net(state)
        mean = mean * 2  # Scale to [-2, 2] for Pendulum (non-in-place)

        x = F.relu(state)
        log_std = self.log_std(x)

        log_std = torch.clamp(log_std, -20, 0)
        return mean, log_std

    def get_action(self, state):
        """Sample action from the policy"""
        
        mean, log_std = self.forward(state)
        std = torch.exp(log_std)
        dist = torch.distributions.Normal(mean, std)
        action = dist.sample()
        log_prob = dist.log_prob(action)

        action = torch.clamp(action, -2.0, 2.0)
        return action.detach(), log_prob.detach()

Actor Network - CSY

Critic Network

class Critic(nn.Module):
    """Critic network that estimates state value function V(s)"""

    def __init__(self, state_dim, hidden_dim=128):
        super(Critic, self).__init__()
        self.value_net = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 1)
        )

    def forward(self, state):
        return self.value_net(state)

Critic Network - CSY

Actor Critic Agent

class ActorCritic:
    """Actor-Critic algorithm implementation"""

    def __init__(self, state_dim, action_dim, lr_actor=1e-4, lr_critic=3e-4, gamma=0.99):
        self.gamma = gamma

        self.actor = Actor(state_dim, action_dim)
        self.critic = Critic(state_dim)
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=lr_actor)
        self.critic_optimizer = optim.Adam(
            self.critic.parameters(), lr=lr_critic)

        self.reward_mean = 0.0
        self.reward_std = 1.0
        self.reward_count = 0

    def update(self, states, actions, rewards, next_states, dones):
        """Update both actor and critic networks"""

        states = torch.FloatTensor(np.array(states))
        actions = torch.FloatTensor(np.array(actions))

        rewards = torch.FloatTensor(np.array(rewards))

        next_states = torch.FloatTensor(np.array(next_states))
        dones = torch.BoolTensor(np.array(dones))

        values = self.critic(states).squeeze()
        next_values = self.critic(next_states).squeeze()

        td_targets = rewards + self.gamma * next_values * (~dones)
        advantages = td_targets - values

        for _ in range(2):
            critic_loss = F.mse_loss(values, td_targets.detach())
            self.critic_optimizer.zero_grad()
            critic_loss.backward(retain_graph=True)

            torch.nn.utils.clip_grad_norm_(
                self.critic.parameters(), max_norm=1.0)
            self.critic_optimizer.step()

            values = self.critic(states).squeeze()

        mean, log_std = self.actor(states)
        std = torch.exp(log_std)
        dist = torch.distributions.Normal(mean, std)
        log_probs = dist.log_prob(actions).sum(dim=-1)

        
        actor_loss = -(log_probs * advantages.detach()).mean() - 0.01
        self.actor_optimizer.zero_grad()
        actor_loss.backward()

        torch.nn.utils.clip_grad_norm_(self.actor.parameters(), max_norm=1.0)
        self.actor_optimizer.step()

        return actor_loss.item(), critic_loss.item()

Actor Critic Agent - CSY

Finally, we combine all the core parts together to run the agent with Pendulum environment.

def main():
    
    # Environment setup
    env = gym.make('Pendulum-v1')
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.shape[0]

    # Initialize agent
    agent = ActorCritic(state_dim, action_dim)

    # Training parameters
    num_episodes = 5000
    max_steps = 200
    update_frequency = 64  # Less frequent updates for stability

    # Tracking variables
    episode_rewards = []
    critic_losses = []
    actor_losses = []
    recent_rewards = deque(maxlen=100)

    # Storage for batch updates
    states_batch = []
    actions_batch = []
    rewards_batch = []
    next_states_batch = []
    dones_batch = []

    print("Starting Actor-Critic training on Pendulum-v1...")
    print(f"State dimension: {state_dim}, Action dimension: {action_dim}")
    print("Key improvements: Advantage normalization, reward normalization, gradient clipping, entropy bonus")

    for episode in range(num_episodes):
        state, _ = env.reset()
        episode_reward = 0

        for _ in range(max_steps):
            # Get action from actor

            state_tensor = torch.FloatTensor(state).unsqueeze(0)
            action, log_prob = agent.actor.get_action(state_tensor)
            action_np = action.numpy().flatten()

            next_state, reward, terminated, truncated, _ = env.step(action_np)
            done = terminated or truncated

            # Store experience
            states_batch.append(state)
            actions_batch.append(action_np)
            rewards_batch.append(reward)
            next_states_batch.append(next_state)
            dones_batch.append(done)

            episode_reward += reward
            state = next_state

            # Update networks when batch is full
            if len(states_batch) >= update_frequency:
                actor_loss, critic_loss = agent.update(
                    states_batch, actions_batch, rewards_batch,
                    next_states_batch, dones_batch
                )
                actor_losses.append(actor_loss)
                critic_losses.append(critic_loss)

                # Clear batch
                states_batch.clear()
                actions_batch.clear()
                rewards_batch.clear()
                next_states_batch.clear()
                dones_batch.clear()

            if done:
                break

        episode_rewards.append(episode_reward)
        recent_rewards.append(episode_reward)

    env.close()
    return episode_rewards, critic_losses, actor_losses

Actor Critic - CSY

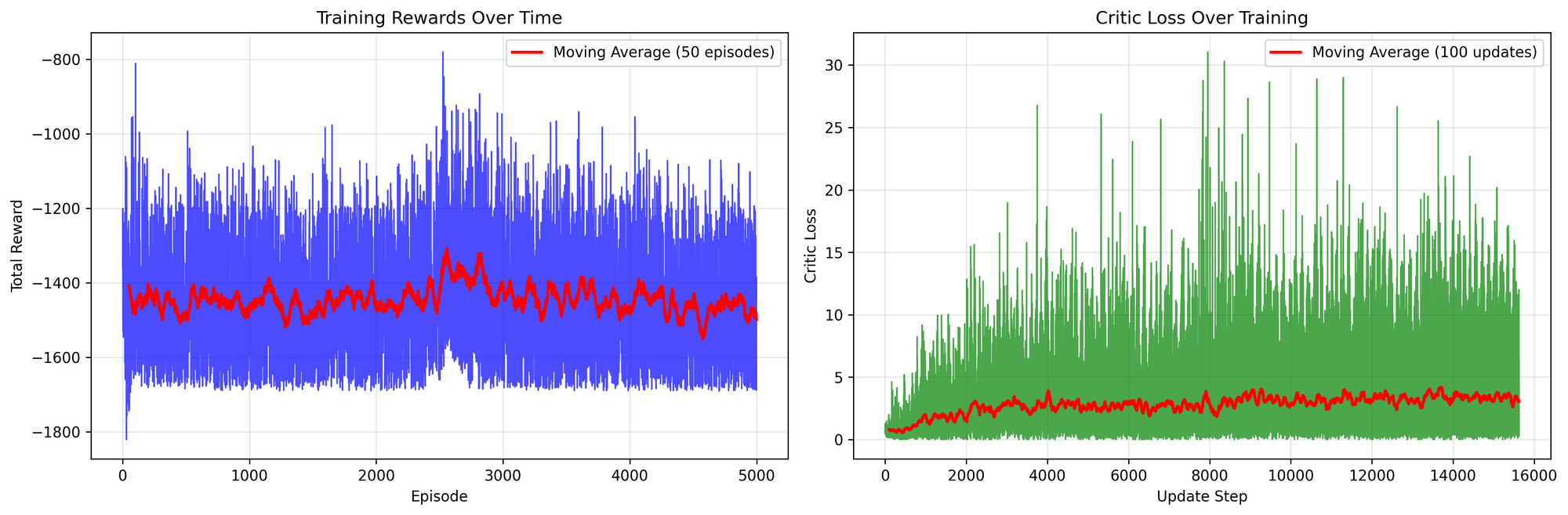
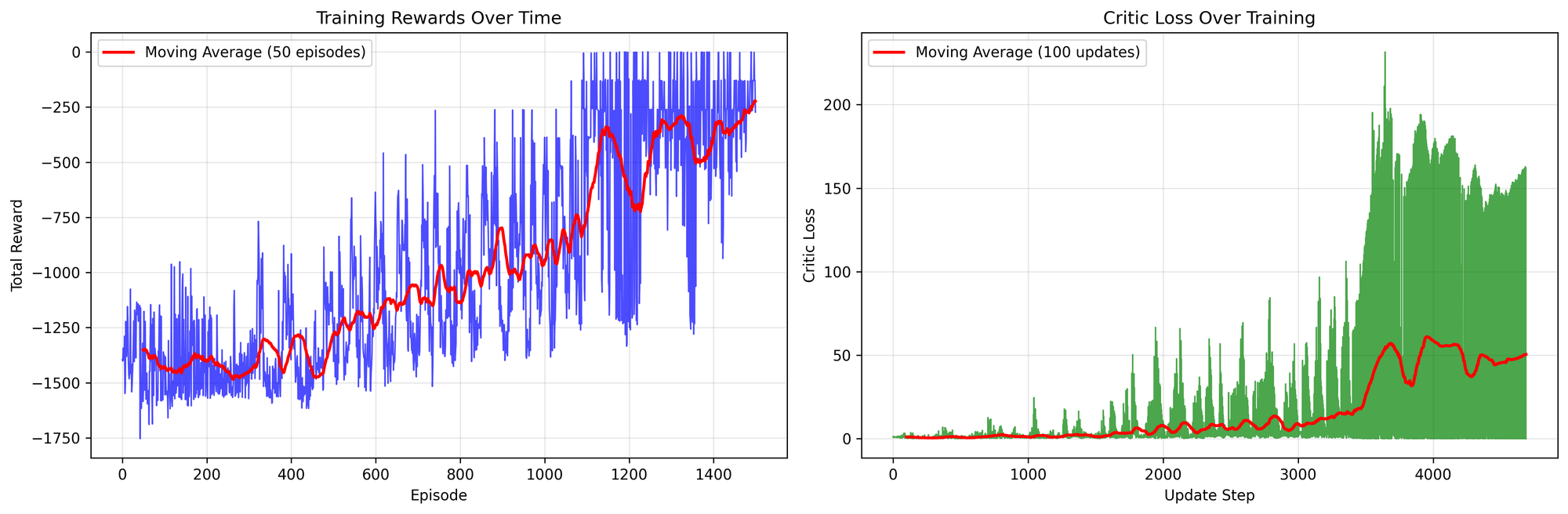
Training without Normalization - CSY
Training with Normalization -CSY

Clearly, as shown in the diagram above, normalizing the rewards during training leads to better results within 1,300 episodes.

Conclusion

The Actor-Critic structure is powerful because it combines both policy-based and value-based approaches. This hybrid design leverages the strengths of each method while mitigating their individual weaknesses. Moreover, it serves as the foundation for more advanced algorithms that significantly outperform earlier methods.

Importantly, the Actor-Critic framework demonstrates that different approaches can work effectively when combined, opening the door to integrating more complex networks that can yield accurate yet simple decision-making.

CSY

CSY

Nagoya, Japan