Image Compression - JPEG(I)

Today, we’re going to talk about image compression—specifically JPEG, one of the most commonly used image formats today. To keep things manageable, we’ll split this topic into two posts.
So, why do we need JPEG, and how does it work? Simply put, JPEG uses the Discrete Cosine Transform (DCT), which we discussed in the Frequency Analysis section, to achieve compression by removing information that is difficult for the human eye to perceive. Here are some key reasons:
- Redundancy
- Images are not random signals
- Neighboring pixels are likely to take similar values and correlated
Assuming that a transform should concentrate the important information, this brings to mind the use of the DCT.
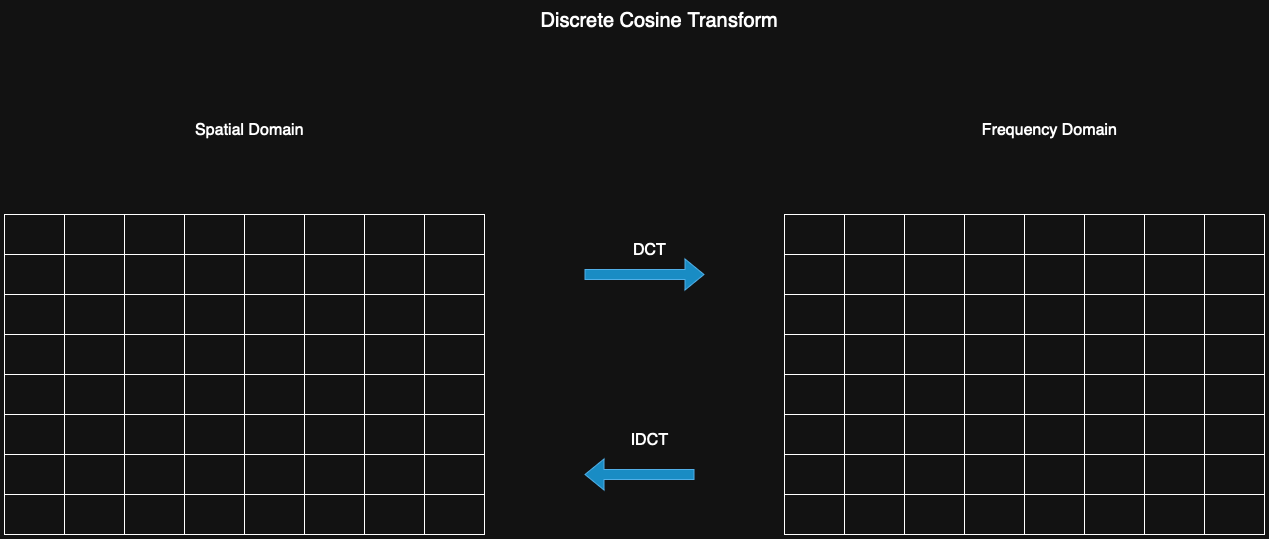
We will use 8 × 8 pixel blocks to apply the DCT and IDCT, and observe how this process affects images. For reference, the mathematical definition is provided below:
$$F(k,l) = \sum_{n=0}^7 \sum_{m=0}^7 \dfrac{C(k)C(l)}{4} f(m,n) \cos{(\dfrac{\pi}{16}(2m+1)k)} \cos{(\dfrac{\pi}{16}(2n+1)l)}$$
$$f(m,n) = \sum_{k=0}^7 \sum_{l=0}^7 \dfrac{C(k)C(l)}{4} F(k,l) \cos{(\dfrac{\pi}{16}(2m+1)k)} \cos{(\dfrac{\pi}{16}(2n+1)l)}$$
where:
$$C(i) = \begin{cases} 1 & i \ne 0 \\ 1/\sqrt{2} & i = 0 \end{cases}$$
The equations above are implemented as follows:
void DCT8x8(double input[8][8], double output[8][8]) {
for (int l = 0; l < 8; l++) {
for (int k = 0; k < 8; k++) {
double value = 0.0;
for (int n = 0; n < 8; n++) {
for (int m = 0; m < 8; m++) {
double Cx = 1.0;
double Cy = 1.0;
double cosx = cos(M_PI * (2 * m + 1) * k / 16);
double cosy = cos(M_PI * (2 * n + 1) * l / 16);
if (k == 0)
Cx = 1 / sqrt(2.0);
if (l == 0)
Cy = 1 / sqrt(2.0);
double temp = input[m][n];
temp = temp * cosx * cosy * Cx * Cy / 4;
value = value + temp;
}
}
output[k][l] = value;
}
}
}
void IDCT8x8(double input[8][8], double output[8][8]) {
for (int n = 0; n < 8; n++) {
for (int m = 0; m < 8; m++) {
double value = 0.0;
for (int l = 0; l < 8; l++) {
for (int k = 0; k < 8; k++) {
double Cx = 1.0;
double Cy = 1.0;
double cosx = cos(M_PI * (2 * m + 1) * k / 16);
double cosy = cos(M_PI * (2 * n + 1) * l / 16);
if (k == 0)
Cx = 1 / sqrt(2.0);
if (l == 0)
Cy = 1 / sqrt(2.0);
double temp = input[k][l];
temp = temp * cosx * cosy * Cx * Cy / 4;
value = value + temp;
}
}
output[m][n] = value;
}
}
}DCT-IDCT Code - CSY
Clearly, these two code snippets follow the underlying equation. One important detail to note is that the process operates on individual image blocks. Therefore, we need to update the image header code we’ve used so far to include block division functionality. Below is a partial code snippet; you can refer to the full implementation in the codebase for more details.
void Image::divide(int size) {
printf("Image divided into %dx%d blocks of size %dx%d\n",
getBlockCountX(size), getBlockCountY(size), size, size);
}
int Image::getBlockCountX(int blockSize) {
return (this->mW + blockSize - 1) / blockSize;
}
int Image::getBlockCountY(int blockSize) {
return (this->mH + blockSize - 1) / blockSize;
}Image Block Separation - CSY
The first task is to apply the DCT followed by the IDCT to verify whether we can restore the original image within an acceptable threshold. This threshold helps us determine if significant data loss has occurred during the process. Let’s take a look at the code:
void dct_idct(Image *in, Image *out) {
printf("Starting DCT+IDCT...\n");
in->divide(8);
int total_blocks = in->getBlockCountX(8) * in->getBlockCountY(8);
int processed_blocks = 0;
for (int block_y = 0; block_y < in->getBlockCountY(8); ++block_y) {
for (int block_x = 0; block_x < in->getBlockCountX(8); ++block_x) {
Image block;
in->getBlock(block_x, block_y, 8, block);
double input_block[8][8];
double dct_coeffs[8][8];
double reconstructed_block[8][8];
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
if (x < block.getWidth() && y < block.getHeight()) {
if (block.getCH() == 1) {
input_block[y][x] = block.get(x, y) - 128.0;
} else {
input_block[y][x] = block.get(x, y, 0) - 128.0;
}
} else {
input_block[y][x] = 0.0;
}
}
}
DCT8x8(input_block, dct_coeffs);
IDCT8x8(dct_coeffs, reconstructed_block);
Image restored_block;
restored_block.init(
block.getWidth(), block.getHeight(), block.getCH());
for (int y = 0; y < block.getHeight(); ++y) {
for (int x = 0; x < block.getWidth(); ++x) {
double pixel_value = reconstructed_block[y][x] + 128.0;
pixel_value = fmax(0, fmin(255, pixel_value));
if (block.getCH() == 1) {
restored_block.set(x, y, pixel_value);
} else {
for (int ch = 0; ch < block.getCH(); ch++) {
restored_block.set(x, y, ch, pixel_value);
}
}
}
}
out->setBlock(block_x, block_y, 8, restored_block);
++processed_blocks;
if (processed_blocks % 10 == 0) {
printf("Processed %d/%d blocks\n", processed_blocks, total_blocks);
}
}
}
printf("\n=== DCT+IDCT Verification ===\n");
printf("✓ Applied DCT followed by IDCT to all blocks\n");
printf("✓ Confirms that DCT is a reversible transform!\n");
verify_dct_idct(in, out);
}DCT-IDCT - CSY
As the first step, we calculate how many blocks we need to process. Then, for each block, we apply the Discrete Cosine Transform (DCT) and its inverse (IDCT) to obtain the transformed and restored values. The restored_block stores the values produced by the IDCT, and we reconstruct the original image by processing each block using setBlock. That’s the basic idea.
Additionally, to visualize the transformation, I applied the DCT and generated a visual representation of the result. The corresponding code is shown below:
void dct_visualize(Image *in, Image *out) {
printf("Starting DCT visualization...\n");
in->divide(8);
int total_blocks = in->getBlockCountX(8) * in->getBlockCountY(8);
int processed_blocks = 0;
for (int block_y = 0; block_y < in->getBlockCountY(8); ++block_y) {
for (int block_x = 0; block_x < in->getBlockCountX(8); ++block_x) {
Image block;
in->getBlock(block_x, block_y, 8, block);
double input_block[8][8];
double dct_coeffs[8][8];
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
if (x < block.getWidth() && y < block.getHeight()) {
if (block.getCH() == 1) {
input_block[y][x] = block.get(x, y) - 128.0;
} else {
input_block[y][x] = block.get(x, y, 0) - 128.0;
}
} else {
input_block[y][x] = 0.0;
}
}
}
DCT8x8(input_block, dct_coeffs);
double max_coeff = 0.0;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
if (fabs(dct_coeffs[y][x]) > max_coeff) {
max_coeff = fabs(dct_coeffs[y][x]);
}
}
}
int block_start_x = block_x * 8;
int block_start_y = block_y * 8;
for (int y = 0; y < block.getHeight() && y < 8; y++) {
for (int x = 0; x < block.getWidth() && x < 8; x++) {
double normalized;
if (max_coeff > 0) {
normalized = (dct_coeffs[y][x] / max_coeff) * 127.5 + 127.5;
} else {
normalized = 127.5;
}
normalized = fmax(0, fmin(255, normalized));
out->set(block_start_x + x, block_start_y + y, normalized);
}
}
}
}
printf("\n=== DCT Visualization Complete ===\n");
printf("✓ DCT coefficients visualized for all blocks\n");
}
DCT Visualization - CSY
In the visualization, we need to normalize the coefficient values to the range [0,255] as defined below:
$$n = \dfrac{\text {coef} }{\text {max coef} } \cdot 127.5 + 127.5$$
Let's view the results.

Figure 1-1: Original
Figure 1-2: DFT Visual

Figure 1-3: Restored
To better understand how frequency represents an image, I performed an analysis to highlight the differences between low-frequency and high-frequency components.
typedef struct {
int x, y;
double energy;
double percentage;
} CoeffEnergy;
void dct_energy(Image *in, Image *out) {
printf("Starting DCT energy calculation...\n");
int block_count = 0;
double total_energy[8][8] = {0};
in->divide(8);
int total_blocks = in->getBlockCountX(8) * in->getBlockCountY(8);
int processed_blocks = 0;
for (int block_y = 0; block_y < in->getBlockCountY(8); ++block_y) {
for (int block_x = 0; block_x < in->getBlockCountX(8); ++block_x) {
Image block;
in->getBlock(block_x, block_y, 8, block);
double input_block[8][8];
double dct_coeffs[8][8];
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
if (x < block.getWidth() && y < block.getHeight()) {
if (block.getCH() == 1) {
input_block[y][x] = block.get(x, y) - 128.0;
} else {
input_block[y][x] = block.get(x, y, 0) - 128.0;
}
} else {
input_block[y][x] = 0.0;
}
}
}
DCT8x8(input_block, dct_coeffs);
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
total_energy[y][x] += dct_coeffs[y][x] * dct_coeffs[y][x];
}
}
block_count++;
++processed_blocks;
if (processed_blocks % 10 == 0) {
printf("Processed %d/%d blocks\n", processed_blocks, total_blocks);
}
}
}
double avg_energy[8][8];
double total_sum = 0.0;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
avg_energy[y][x] = total_energy[y][x] / block_count;
total_sum += avg_energy[y][x];
}
}
CoeffEnergy coeffs[64];
int idx = 0;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
coeffs[idx].x = x;
coeffs[idx].y = y;
coeffs[idx].energy = avg_energy[y][x];
coeffs[idx].percentage = (avg_energy[y][x] / total_sum) * 100.0;
idx++;
}
}
for (int i = 0; i < 64 - 1; i++) {
for (int j = 0; j < 64 - i - 1; j++) {
if (coeffs[j].energy < coeffs[j + 1].energy) {
CoeffEnergy temp = coeffs[j];
coeffs[j] = coeffs[j + 1];
coeffs[j + 1] = temp;
}
}
}
double low_freq_energy = 0.0;
double mid_freq_energy = 0.0;
double high_freq_energy = 0.0;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
if (x < 4 && y < 4) {
low_freq_energy += avg_energy[y][x];
} else if (x >= 4 && y >= 4) {
high_freq_energy += avg_energy[y][x];
} else {
mid_freq_energy += avg_energy[y][x];
}
}
}
Image *energy_img = new Image();
energy_img->init(8, 8, 1);
double max_energy = coeffs[0].energy;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
double normalized = (avg_energy[y][x] / max_energy) * 255.0;
energy_img->set(x, y, normalized);
}
}
printf("\n=== DCT Energy Analysis ===\n");
printf("Total blocks analyzed: %d\n", block_count);
printf("Total average energy: %.2f\n\n", total_sum);
printf("Top 10 DCT coefficients by energy:\n");
printf("Rank\tPosition\tAvg Energy\tPercentage\n");
printf("----\t--------\t----------\t----------\n");
for (int i = 0; i < 10; i++) {
printf("%d\t(%d,%d)\t\t%.2f\t\t%.2f%%\n", i + 1, coeffs[i].x, coeffs[i].y,
coeffs[i].energy, coeffs[i].percentage);
}
printf("\nFrequency Band Energy Distribution:\n");
printf("Low frequencies (0-3, 0-3): %.2f%% of total energy\n",
(low_freq_energy / total_sum) * 100);
printf("Mid frequencies: %.2f%% of total energy\n",
(mid_freq_energy / total_sum) * 100);
printf("High frequencies (4-7, 4-7): %.2f%% of total energy\n",
(high_freq_energy / total_sum) * 100);
printf("\nDC coefficient (0,0) analysis:\n");
printf("DC energy: %.2f (%.2f%% of total)\n", avg_energy[0][0],
(avg_energy[0][0] / total_sum) * 100);
printf("\nEnergy compaction analysis:\n");
double cumulative_energy = 0.0;
int coeffs_for_90_percent = 0;
int coeffs_for_95_percent = 0;
int coeffs_for_99_percent = 0;
for (int i = 0; i < 64; i++) {
cumulative_energy += coeffs[i].energy;
double cumulative_percentage = (cumulative_energy / total_sum) * 100.0;
if (cumulative_percentage >= 90.0 && coeffs_for_90_percent == 0) {
coeffs_for_90_percent = i + 1;
}
if (cumulative_percentage >= 95.0 && coeffs_for_95_percent == 0) {
coeffs_for_95_percent = i + 1;
}
if (cumulative_percentage >= 99.0 && coeffs_for_99_percent == 0) {
coeffs_for_99_percent = i + 1;
}
}
printf("Coefficients needed for 90%% of energy: %d/64 (%.1f%%)\n",
coeffs_for_90_percent, (coeffs_for_90_percent / 64.0) * 100);
printf("Coefficients needed for 95%% of energy: %d/64 (%.1f%%)\n",
coeffs_for_95_percent, (coeffs_for_95_percent / 64.0) * 100);
printf("Coefficients needed for 99%% of energy: %d/64 (%.1f%%)\n",
coeffs_for_99_percent, (coeffs_for_99_percent / 64.0) * 100);
printf("\n=== Analysis Complete ===\n");
printf("✓ This demonstrates DCT's energy compaction property\n");
printf("✓ Most energy is concentrated in low-frequency coefficients\n");
printf("✓ High-frequency coefficients can be discarded for compression\n");
delete energy_img;
}DCT Energy Analysis - CSY
Using this function, we apply it to the boat image shown above and obtain the results below:
=== DCT Energy Analysis ===
Total blocks analyzed: 1024
Total average energy: 87359.89
Top 10 DCT coefficients by energy:
Rank Position Avg Energy Percentage
---- -------- ---------- ----------
1 (0,0) 58760.34 67.26%
2 (1,0) 9141.68 10.46%
3 (0,1) 5431.83 6.22%
4 (2,0) 3066.88 3.51%
5 (1,1) 1930.86 2.21%
6 (3,0) 1275.05 1.46%
7 (2,1) 1088.13 1.25%
8 (0,2) 1023.04 1.17%
9 (4,0) 767.23 0.88%
10 (5,0) 598.33 0.68%
Frequency Band Energy Distribution:
Low frequencies (0-3, 0-3): 96.02% of total energy
Mid frequencies: 3.85% of total energy
High frequencies (4-7, 4-7): 0.12% of total energy
DC coefficient (0,0) analysis:
DC energy: 58760.34 (67.26% of total)
Energy compaction analysis:
Coefficients needed for 90% of energy: 6/64 (9.4%)
Coefficients needed for 95% of energy: 10/64 (15.6%)
Coefficients needed for 99% of energy: 23/64 (35.9%)
=== Analysis Complete ===
✓ This demonstrates DCT's energy compaction property
✓ Most energy is concentrated in low-frequency coefficients
✓ High-frequency coefficients can be discarded for compressionNow that we understand the basics, it's clear that most of the energy in an image is concentrated in the lower frequencies.
Conclusion
We have seen how JPEG uses the DCT to achieve image compression. Once you understand how to transform an image from the spatial domain to the frequency domain, the process becomes much clearer. While there are more advanced techniques designed for various purposes, the core idea remains the same.



