Image Histogram and Equalization

Today, we’re going to analyze an image by focusing on its pixels. You can think of pixels as the fundamental elements that compose the image—much like how matter is made up of various natural elements in the universe. An image is no longer something mysterious; let’s unravel its structure together.
Image Histogram
Histogram: A graphical representation of the distribution of a dataset. It visualizes the frequency of data values grouped into specified ranges called bins.
Based on the definition, it’s clear that we count the number of pixels for each value—in the case of a grayscale image, from 0 to 255. What’s really important is that we convert the image into numerical data and view it from the perspective of frequency and distribution. Why does knowing the frequency help us so much? Because hidden within the frequency data are patterns worth exploring or adjusting based on mathematical principles.
Here’s how you can display a histogram of an image. You can find the codebase here. This code supports both grayscale and RGB images.
void histogram(Image *in, Image *out, int binsize, FILE *fp) {
int W = in->getWidth();
int H = in->getHeight();
int C = in->getCH();
int nBins = 256 / binsize;
if (C == 1) {
int *histdata = new int[nBins];
for (int idx = 0; idx < nBins; idx++) {
histdata[idx] = 0;
}
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int value = in->get(x, y);
int bin = value / binsize;
histdata[bin]++;
}
}
for (int idx = 0; idx < nBins; idx++) {
int mid = idx * binsize + binsize / 2;
fprintf(fp, "[%.03d-%.03d]\t", idx * binsize, (idx + 1) * binsize - 1);
int num = histdata[idx];
int denom = 0.1 * W * H / nBins;
for (int cnt = 0; cnt < num / denom; cnt++) {
fprintf(fp, "*");
}
fprintf(fp, "\n");
}
} else {
int *r_histdata = new int[nBins];
int *g_histdata = new int[nBins];
int *b_histdata = new int[nBins];
for (int idx = 0; idx < nBins; idx++) {
r_histdata[idx] = 0;
g_histdata[idx] = 0;
b_histdata[idx] = 0;
}
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int rvalue = in->get(x, y, 0);
int gvalue = in->get(x, y, 1);
int bvalue = in->get(x, y, 2);
r_histdata[rvalue]++;
g_histdata[gvalue]++;
b_histdata[bvalue]++;
}
}
for (int idx = 0; idx < nBins; idx++) {
int mid = idx * binsize + binsize / 2;
fprintf(fp, "%d\t%d\n", mid, r_histdata[idx]);
fprintf(fp, "%d\t%d\n", mid, g_histdata[idx]);
fprintf(fp, "%d\t%d\n", mid, b_histdata[idx]);
}
}
}Histogram - CSY
When using a binsize = 1, you get a detailed count of each pixel value from 0 to 255. The output file looks like this:
...omitted
[100-100] *********
[101-101] **********
[102-102] *********
[103-103] *********
[104-104] ********
[105-105] *********
[106-106] ********
[107-107] **********
[108-108] ********
[109-109] *********
[110-110] **********
[111-111] *********
[112-112] *********
[113-113] **********
[114-114] *********
[115-115] ***********
[116-116] *********
[117-117] ***********
[118-118] ************
[119-119] ************
[120-120] ************
...omittedBin Count - CSY

Figure 1-1: Image
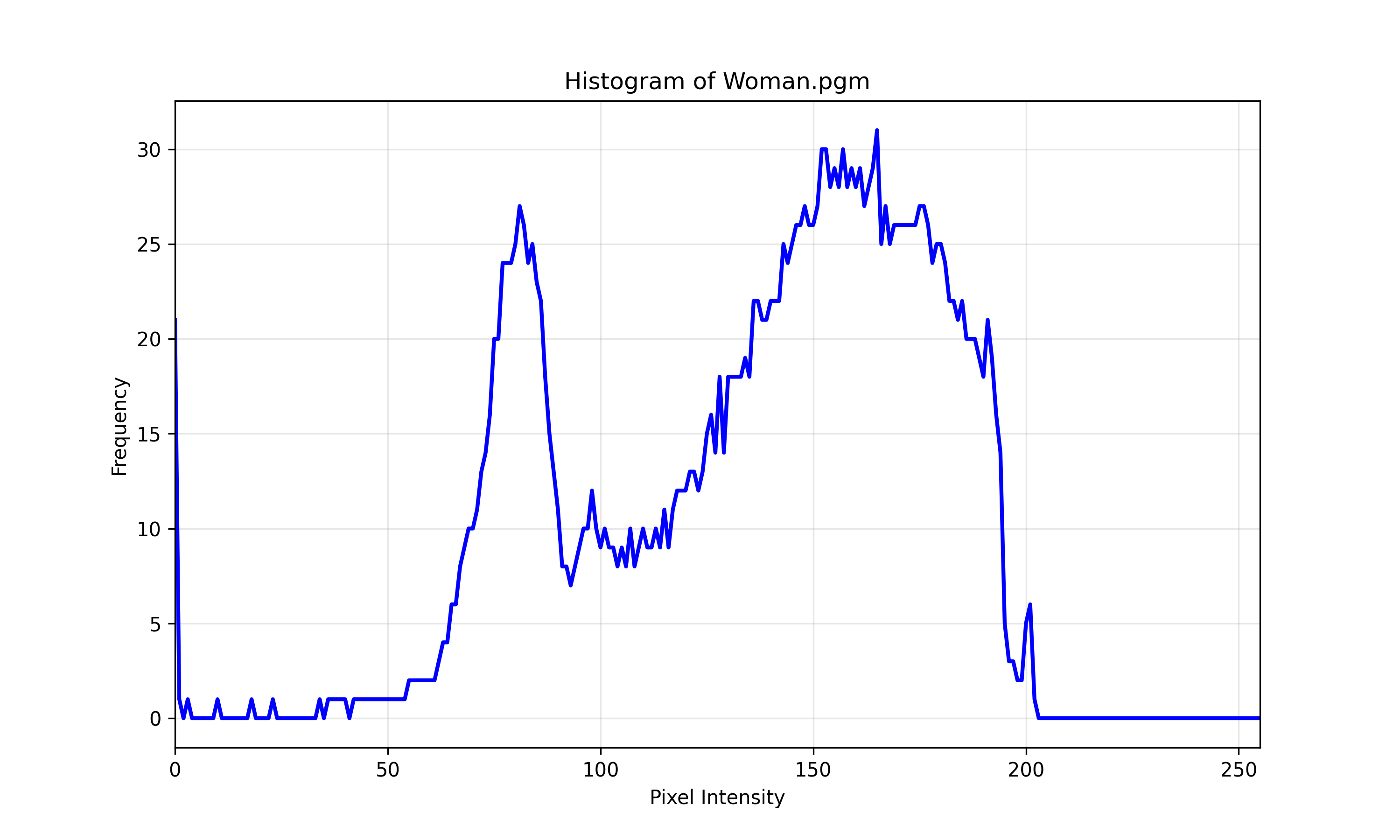
Figure 1-2: binsize = 1
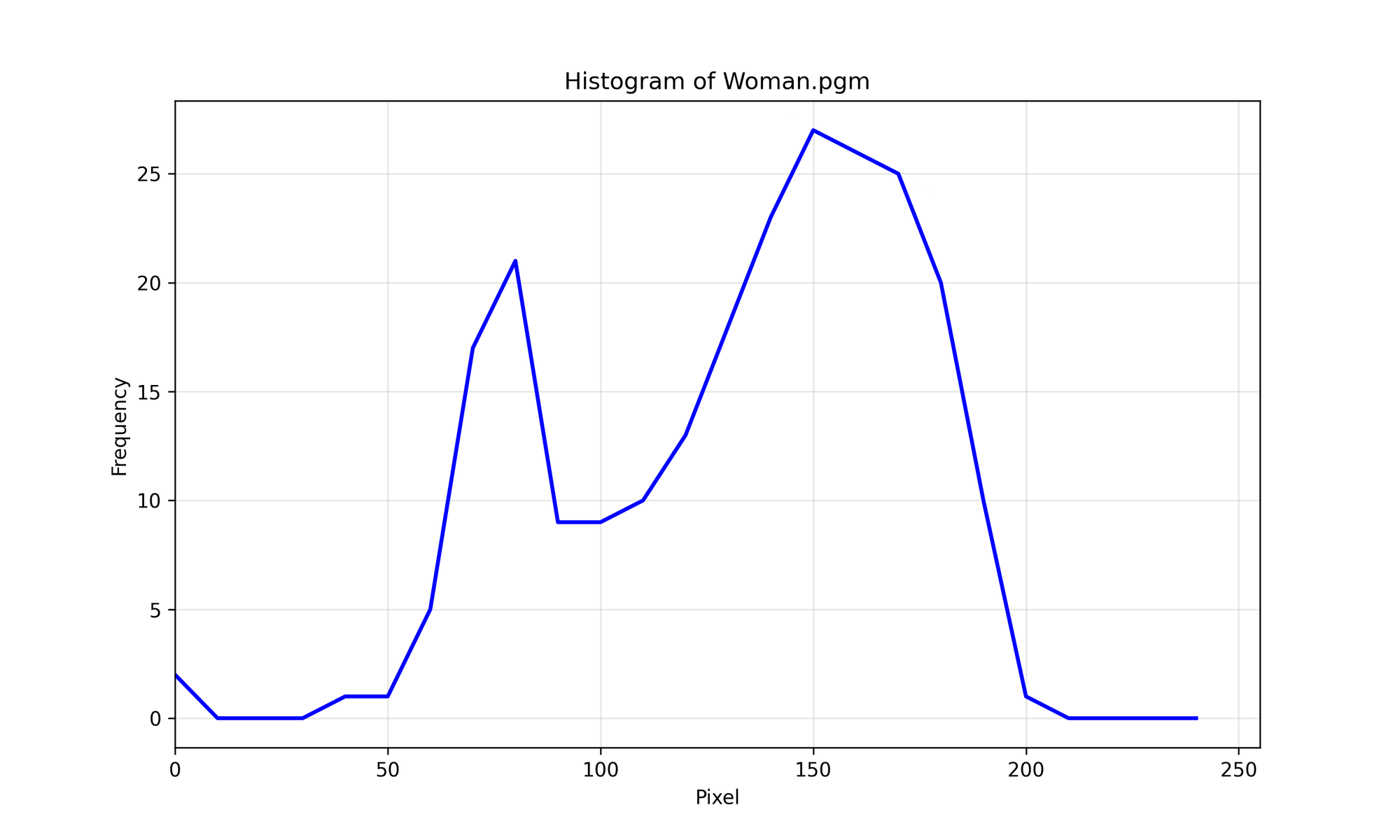
Figure 1-3: binsize = 10
It’s probably a good idea to think of the bin size as a kind of smoothing hyperparameter. Now, let’s dive into Histogram Equalization.
Histogram Equalization
Histogram equalization is a technique used to enhance contrast in an image by redistributing pixel intensities. It spreads out the most frequent intensity values, making dark areas lighter and bright areas darker.
In images with poor contrast, many pixel values are clustered within a narrow range—either mostly dark or mostly light. This operation redistributes the intensity values to create a more uniform distribution, which makes details more distinguishable.
Here are the steps and the mathematical formulation:
- Compute the histogram of the image
- Calculate the cumulative distribution function (CDF)
- Normalize the CDF
- Map the original pixel using the created CDF table
$$T(r) = round((L - 1) \cdot \text{CDF}(r))$$
- $r$: original intensity of pixels
- $L$: gray levels (256 in our case)
- $CDF$: cumulative distribution function
Note: This method works best on grayscale images.
Let’s first look at the code and the results, then discuss why it doesn’t work well for RGB images.
void histogram_equalization(Image *in, Image *out, int binsize, FILE *fp) {
// binsize if not needed here, but for convenience it is kept
int W = in->getWidth();
int H = in->getHeight();
int C = in->getCH();
int histdata[256] = {0};
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int value = in->get(x, y);
histdata[value]++;
}
}
int cdf[256] = {0};
cdf[0] = histdata[0];
for (int i = 1; i < 256; i++) {
cdf[i] = cdf[i - 1] + histdata[i];
}
int cdf_min = 0;
for (int i = 0; i < 256; i++) {
if (cdf[i] != 0) {
cdf_min = cdf[i];
break;
}
}
int table[256];
for (int i = 0; i < 256; i++) {
if (cdf[i] == 0) {
table[i] = 0;
fprintf(fp, "%d\t0\n", i);
} else {
double equalized =
round(((cdf[i] - cdf_min) * 255.0) / (W * H - cdf_min));
table[i] = (int)equalized;
fprintf(fp, "%d\t%d\n", i, table[i]);
}
}
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int original_value = in->get(x, y);
int equalized_value = table[original_value];
out->set(x, y, equalized_value);
}
}
}Histogram Equalization - CSY
The CDF table can be easily calculated. From the code snippet, you can see that the mapping is calculated and normalized. Note that cdf_min is subtracted because, in this mapping, a value of cdf[i] = 0 corresponds to the absence of information in that part of the image. Here is the difference:

Figure 2-1: Origin

Figure 2-2: Equalization
Luminance Equalization
So, why can’t this be directly applied to RGB images?
The reason is color distortion. Each RGB channel contains both brightness and color information. If you apply equalization separately to the R, G, and B channels, it alters the intensity and changes the relative balance between the channels, resulting in unnatural colors.
Example:
R: 120, G: 80, B: 80 → R:180, G:250, B: 100
This breaks the original color balance. However, there is a solution called Luminance Channel Equalization, which involves converting the RGB image to a luminance-based color space, such as HSV or YUV. Let’s apply this method to RGB images. The conversion formulas are listed below.
RGB to YUV
$$\begin{cases} Y = 0.299R + 0.587G + 0.114B \\ U = -0.169R - 0.331G + 0.500B \\ V = 0.500R - 0.419G - 0.081B \end{cases}$$
YUV to RGB
$$\begin{cases} R = 1.000Y + 1.402V \\ G = 1.000Y - 0.344U - 0.714V \\ B = 1.000Y + 1.772U \end{cases}$$
Using this formula, we can apply it in the code and observe the results on an RGB image.
void histogram_equalization(Image *in, Image *out, int binsize, FILE *fp) {
// ...omitted
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
double r_value = in->get(x, y, 0);
double g_value = in->get(x, y, 1);
double b_value = in->get(x, y, 2);
double y_value = 0.299 * r_value + 0.587 * g_value + 0.114 * b_value;
double u_value =
-0.1687 * r_value - 0.331 * g_value + 0.5 * b_value + 128;
double v_value =
0.5 * r_value - 0.419 * g_value - 0.081 * b_value + 128;
out->set(x, y, 0, y_value);
out->set(x, y, 1, u_value);
out->set(x, y, 2, v_value);
}
}
int histdata[256] = {0};
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int value = out->get(x, y, 0);
histdata[value]++;
}
}
int cdf[256] = {0};
cdf[0] = histdata[0];
for (int i = 1; i < 256; i++) {
cdf[i] = cdf[i - 1] + histdata[i];
}
int cdf_min = 0;
for (int i = 0; i < 256; i++) {
if (cdf[i] != 0) {
cdf_min = cdf[i];
break;
}
}
int table[256];
for (int i = 0; i < 256; i++) {
if (cdf[i] == 0) {
table[i] = 0;
fprintf(fp, "%d\t0\n", i);
} else {
double equalized =
round(((cdf[i] - cdf_min) * 255.0) / (W * H - cdf_min));
table[i] = (int)equalized;
fprintf(fp, "%d\t%d\n", i, table[i]);
}
}
// Apply equalization to Y channel in output image
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
int original_value = out->get(x, y, 0);
int equalized_value = table[original_value];
out->set(x, y, 0, equalized_value);
}
}
// Convert from YUV to RGB using equalized Y channel
for (int y = 0; y < H; y++) {
for (int x = 0; x < W; x++) {
double y_value = out->get(x, y, 0);
double u_value = out->get(x, y, 1);
double v_value = out->get(x, y, 2);
double r_value = y_value + 1.402 * (v_value - 128);
double g_value =
y_value - 0.34414 * (u_value - 128) - 0.71414 * (v_value - 128);
double b_value = y_value + 1.772 * (u_value - 128);
r_value = std::max(0.0, std::min(255.0, r_value));
g_value = std::max(0.0, std::min(255.0, g_value));
b_value = std::max(0.0, std::min(255.0, b_value));
out->set(x, y, 0, r_value);
out->set(x, y, 1, g_value);
out->set(x, y, 2, b_value);
}
}
}Luminance Equalization - CSY

Figure 3-1: Origin

Figure 3-2: Luminance Equalization
It may not be easy to spot the difference in this image, but the method does work. Take a look at these two examples as well.

Figure 4-1: Origin

Figure 4-2: Luminance Equalization
Conclusion
We've discussed many things in this post, but what stood out to me the most was viewing images in numerical form and performing various operations on them. It sparked an idea—what if we could reverse the process and convert numerical data into image form for reinforcement learning tasks? It’s an intriguing possibility, and I’m excited to explore it further in the future!



