Transformer: Multi-Head Attention

Today, we’re going to dive deeper into the Transformer. However, before discussing its architecture, there's one important concept we need to cover: Multi-Head Attention. If you're not familiar with self-attention, you can check it out here.
Imagine you're at a seminar where several groups are engaged in different conversations. You want to pay attention to multiple discussions that are relevant to your research on reinforcement learning (RL), such as those about model-based algorithms like Dyna-Q and model-free algorithms like PPO.
In this scenario, you might be more interested in PPO algorithms than in Dyna-Q, but you still want to gather some information about Dyna-Q as well. To do this, you would need to attend to both topics—giving more focus to one while still considering the other. This is essentially what multi-head attention does: it allows the model to focus on different parts of the input simultaneously, giving varying levels of importance to each.
Multi-Head Attention Introduction
So, what does multi-head attention look like, and how does it work? Let’s take a look at the following chart, which is a redrawn version from the original paper.
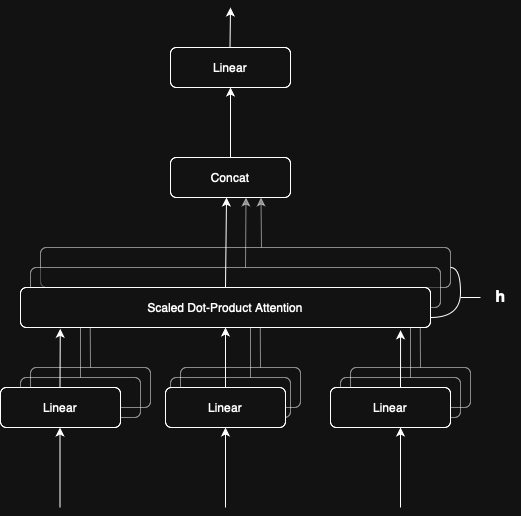
From this diagram, it’s easy to see that we have multiple layers of self-attention. This is similar to how convolutional neural networks (CNNs) use multiple kernels, each serving a distinct purpose such as edge detection or texture recognition when processing image data.
Multi-head attention works in a similar way. It employs multiple attention heads to capture different nuances between tokens, such as syntactic structure or positional relationships in natural language processing (NLP) tasks. However, it's important to note that each attention head operates independently and is unaware of the others.
The formal definition of multi-head attention is written as below.
$$MultiHead(Q,K,V) = Concat(head_1, head_2, ..., head_h)W^Q$$
where each head
$$head_i = Attention(XW_i^Q, XW_i^K, XW_i^V)$$
and
$$Attention(Q,K,V) = softmax(\dfrac{QK^T}{\sqrt{d_k}})V$$
This brings us to an important question: how do we distinguish between the attention heads? Do we need to manually assign each head to focus on a specific pattern? The answer is NO!
What differentiates the heads lies solely in their initial weight matrices. Each head starts with a different set of parameters, and this alone causes them to focus on different aspects of the input.
Personally, this reminds me of the population initialization process in Evolution Strategies, where individuals are generated based on a probabilistic model—such as a Gaussian distribution or a normalized probability distribution. Similarly, the initial random weights in each attention head lead them to explore different patterns and relationships in the data. Let's move to the code.
Mutli-Head Attention Implementation
Now comes the code part. Below, I’ll use 8 heads, which is the hyper-parameter value proposed in the original paper.
import numpy as np
class MultiHeadAttention:
def __init__(self, d_model, num_heads):
assert d_model % num_heads == 0, \
"d_model must be divisible by num_heads"
self.d_model = d_model # Dimension of the model
self.num_heads = num_heads # Number of attention heads
self.d_k = d_model // num_heads # Dimension of each head
# Initialize weight matrices for Query, Key, Value projections
self.W_q = np.random.randn(d_model, d_model) * 0.02
self.W_k = np.random.randn(d_model, d_model) * 0.02
self.W_v = np.random.randn(d_model, d_model) * 0.02
self.W_o = np.random.randn(d_model, d_model) * 0.02
def split_heads(self, x):
"""
Reshape input to separate heads for parallel computation
Args:
x: (batch_size, seq_length, d_model)
Returns:
x: (batch_size, num_heads, seq_length, d_k)
"""
batch_size = x.shape[0]
return x.reshape(batch_size, self.num_heads, -1, self.d_k)
def combine_heads(self, x):
"""
Combine heads back to the original dimension
Args:
x: (batch_size, num_heads, seq_length, d_k)
Returns:
x: (batch_size, seq_length, d_model)
"""
batch_size = x.shape[0]
return x.reshape(batch_size, -1, self.d_model)
def scaled_dot_product_attention(self, Q, K, V):
"""
Calculate scaled dot-product attention
Args:
Q: (batch_size, num_heads, seq_length, d_k)
K: (batch_size, num_heads, seq_length, d_k)
V: (batch_size, num_heads, seq_length, d_k)
Returns:
output: (batch_size, num_heads, seq_length, d_k)
"""
# Query and Key should be transposed to get the dot product
matmul_qk = np.matmul(Q, K.transpose(0, 1, 3, 2))
dk = np.sqrt(self.d_k)
# Scale the attention scores to avoid gradient vanishing
scaled_attention_logits = matmul_qk / dk
# Apply softmax function to get attetion weights sum to 1
attention_weights = \
np.exp(scaled_attention_logits) / \
np.sum(np.exp(scaled_attention_logits),
axis=-1,
keepdims=True
)
output = np.matmul(attention_weights, V)
return output
def forward(self, q, k, v):
# Linear projections and split into heads
q = np.matmul(q, self.W_q)
k = np.matmul(k, self.W_k)
v = np.matmul(v, self.W_v)
q = self.split_heads(q)
k = self.split_heads(k)
v = self.split_heads(v)
# Apply attention
scaled_attention = self.scaled_dot_product_attention(q, k, v)
# Combine heads
concat_attention = self.combine_heads(scaled_attention)
# Final linear projection
output = np.matmul(concat_attention, self.W_o)
return output
if __name__ == "__main__":
d_model = 512 # Model dimension
num_heads = 8 # Number of attention heads
batch_size = 2
seq_length = 10
# Create random input sequences
q = np.random.randn(batch_size, seq_length, d_model)
k = np.random.randn(batch_size, seq_length, d_model)
v = np.random.randn(batch_size, seq_length, d_model)
# Initialize multi-head attention
mha = MultiHeadAttention(d_model, num_heads)
# Forward pass
output = mha.forward(q, k, v)
print(f"Input shape: {q.shape}")
print(f"Output shape: {output.shape}")
print(f"Number of heads: {num_heads}")
print(f"Dimension per head: {d_model // num_heads}")
# print(f"Output: \n {output}")
In the code snippet, we define the model dimension, often referred to as d_model, which represents the embedding dimension used to process input and output vectors. The larger the d_model, the greater the model's capacity to capture complex features—but this also means more parameters to learn.
Next, we move into the multi-head attention mechanism with mha.forward(q, k, v), which kicks off the core process. As you can see, there are some preprocessing steps like split_heads and combine_heads. These are implemented to align with the mathematical formulation of multi-head attention.
During the process, each head independently goes through the self-attention mechanism. Finally, the outputs of all heads are concatenated and passed through an output weight matrix to produce the final result.
Conclusion
Multi-head attention is a powerful mechanism in Transformer models that processes information through multiple parallel heads, each focusing on different aspects of the input simultaneously. Like a team of experts analyzing a complex problem from different angles, each head independently computes attention scores and learns distinct patterns—whether syntactic, semantic, or contextual.
These diverse perspectives are then combined to form a rich, comprehensive representation of the input. This parallel processing approach enables the model to capture complex relationships more effectively than traditional single-head attention, making it particularly valuable for tasks such as natural language processing, machine translation, and text generation. The key innovation lies in its ability to understand and process multiple facets of the data at once, resulting in more nuanced and accurate representations of the input.
What’s even more important is that the mechanism of self-attention seems to be a good fit for reinforcement learning (RL) tasks. It can potentially be applied to trajectories, states, or even the environment itself—helping the agent become more aware of and focus on the most important information.
One never notices what has been done; one can only see what remains to be done. - Marie Curie



