Value/Policy-Based Control

Before diving into corporate reinforcement learning with deep neural networks, it's important to understand two fundamental concepts: the difference between policy-based and value-based approaches, and the distinction between on-policy and off-policy methods.
Value-Based v.s. Policy-Based
What are the difference between these two? Let's check their definition first.
- Value-Based: learn a value function which estimates being in a state when following a certain policy. The policy is derived indirectly by selecting actions that maximize the value function.
- E.g., Q-Learning, SARSA
- Policy-Based: learn a policy, which is a mapping (𝑓: X → Y) from state to actions to dictates what action the agent should take in a given state.
- E.g., REINFORCE, Proximal Policy Optimization (PPO)
The definitions and examples of these concepts are clear, but when I first encountered the terms, I found them confusing—it wasn’t easy to imagine how they applied to real-world problems. If I were to generalize, I’d say value-based methods are like strategists, while policy-based methods are more like improvisers. To truly grasp the difference between them, it's helpful to visualize their behaviors in a familiar setting—such as the classic grid world task.
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple, List
import random
class GridWorld:
def __init__(self, size: int = 3):
self.size = size
self.state = 0 # Start at top-left
self.goal = size * size - 1 # Goal at bottom-right
self.actions = [0, 1, 2, 3] # Up, Right, Down, Left
def reset(self) -> int:
self.state = 0
return self.state
def step(self, action: int) -> Tuple[int, float, bool]:
row = self.state // self.size
col = self.state % self.size
if action == 0: # Up
row = max(0, row - 1)
elif action == 1: # Right
col = min(self.size - 1, col + 1)
elif action == 2: # Downj
row = min(self.size - 1, row + 1)
elif action == 3: # Left
col = max(0, col - 1)
self.state = row * self.size + col
# Reward: -1 for each step, +10 for reaching goal
reward = -1
done = self.state == self.goal
if done:
reward = 10
return self.state, reward, done
class QLearning:
def __init__(self,
n_states: int, n_actions: int,
learning_rate: float = 0.1, gamma: float = 0.99,
epsilon: float = 0.1):
self.q_table = np.zeros((n_states, n_actions))
self.lr = learning_rate
self.gamma = gamma
self.epsilon = epsilon
def choose_action(self, state: int) -> int:
if random.random() < self.epsilon:
return random.choice([0, 1, 2, 3])
return np.argmax(self.q_table[state])
def learn(self, state: int, action: int,
reward: float, next_state: int):
old_value = self.q_table[state, action]
next_max = np.max(self.q_table[next_state])
new_value = (1 - self.lr) * old_value \
+ self.lr * (reward + self.gamma * next_max)
self.q_table[state, action] = new_value
class REINFORCE:
def __init__(self, n_states: int,
n_actions: int, learning_rate: float = 0.01,
gamma: float = 0.99):
# Initialize with uniform distribution
self.policy = np.ones((n_states, n_actions)) / n_actions
self.lr = learning_rate
self.gamma = gamma
def choose_action(self, state: int) -> int:
probs = self.policy[state]
probs = np.maximum(probs, 0)
probs = probs / np.sum(probs)
return np.random.choice(len(probs), p=probs)
def learn(self, states: List[int],
actions: List[int],
rewards: List[float]):
returns = []
G = 0
for r in reversed(rewards):
G = r + self.gamma * G
returns.insert(0, G)
returns = np.array(returns)
returns = (returns - returns.mean()) \
/ (returns.std() + 1e-8) # Normalize returns
for state, action, G in zip(states, actions, returns):
self.policy[state] += self.lr * G * (np.eye(len(self.policy[state]))[action] - self.policy[state])
self.policy[state] = np.maximum(self.policy[state], 0)
self.policy[state] = self.policy[state] \
/ np.sum(self.policy[state])
def train_and_plot():
env = GridWorld()
n_episodes = 1000
n_states = env.size * env.size
n_actions = len(env.actions)
q_agent = QLearning(n_states, n_actions)
q_rewards = []
reinforce_agent = REINFORCE(n_states, n_actions)
reinforce_rewards = []
# Train Q-learning
for _ in range(n_episodes):
state = env.reset()
total_reward = 0
done = False
while not done:
action = q_agent.choose_action(state)
next_state, reward, done = env.step(action)
q_agent.learn(state, action, reward, next_state)
state = next_state
total_reward += reward
q_rewards.append(total_reward)
# Train REINFORCE
for _ in range(n_episodes):
state = env.reset()
states, actions, rewards = [], [], []
done = False
while not done:
action = reinforce_agent.choose_action(state)
next_state, reward, done = env.step(action)
states.append(state)
actions.append(action)
rewards.append(reward)
state = next_state
reinforce_agent.learn(states, actions, rewards)
reinforce_rewards.append(sum(rewards))
# Plot results
plt.figure(figsize=(12, 5))
# Calculate average rewards over 10-episode intervals
def calculate_average_rewards(rewards, interval=10):
return [np.mean(rewards[i:i+interval]) \
for i in range(0, len(rewards), interval)]
q_avg_rewards = calculate_average_rewards(q_rewards)
reinforce_avg_rewards = calculate_average_rewards(reinforce_rewards)
episodes = np.arange(0, n_episodes, 10)
plt.subplot(1, 2, 1)
plt.plot(episodes, q_avg_rewards, label='Q-learning')
plt.title('Q-learning Average Rewards (10-episode intervals)')
plt.xlabel('Episode')
plt.ylabel('Average Reward')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(episodes, reinforce_avg_rewards, label='REINFORCE')
plt.title('REINFORCE Average Rewards (10-episode intervals)')
plt.xlabel('Episode')
plt.ylabel('Average Reward')
plt.legend()
plt.tight_layout()
plt.show()
# Visualize learned policies
def visualize_policy(policy, title):
grid = np.zeros((env.size, env.size))
arrows = ['↑', '→', '↓', '←']
for state in range(n_states):
row = state // env.size
col = state % env.size
action = np.argmax(policy[state])
grid[row, col] = action
plt.figure(figsize=(6, 6))
plt.imshow(grid, cmap='viridis')
plt.title(title)
for i in range(env.size):
for j in range(env.size):
state = i * env.size + j
action = np.argmax(policy[state])
plt.text(j, i, arrows[action],
ha='center', va='center', color='white')
plt.axis('off')
plt.show()
visualize_policy(q_agent.q_table, 'Q-learning Policy')
visualize_policy(reinforce_agent.policy, 'REINFORCE Policy')
if __name__ == "__main__":
train_and_plot()
Value/Policy-Based Comparison - CSY
The code above illustrates how value-based and policy-based methods work, respectively. In particular, you can see the key difference in how they initialize and represent knowledge: value-based methods use a Q-table to store action values, whereas policy-based methods rely on a probability distribution (a uniform distribution, in this case) to guide the agent’s behavior. Let's take a look at the diagrams to visualize this difference more clearly.
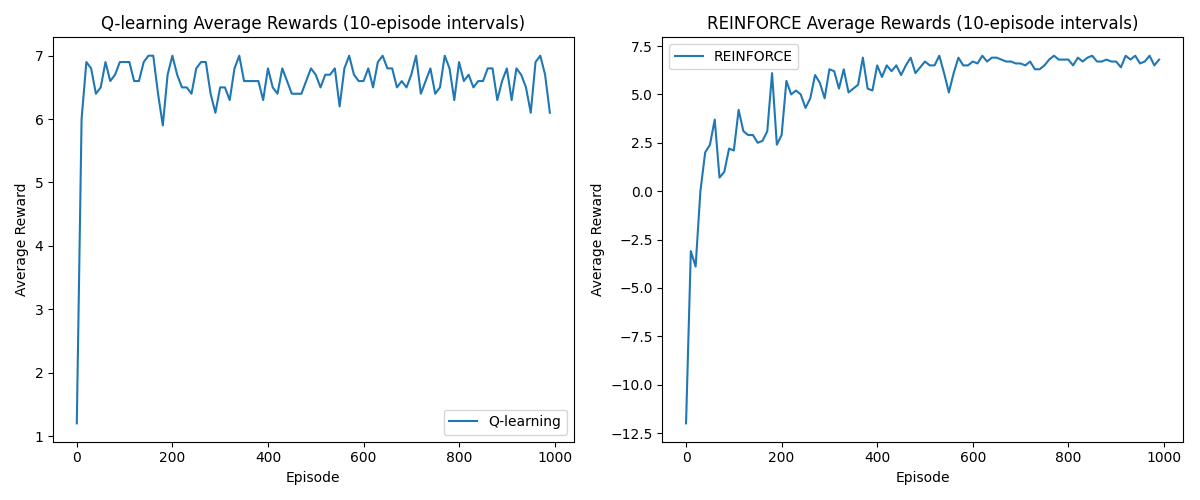
Obviously, both approaches perform well in this grid-world task. However, we observe that the value-based method converges faster than the policy-based one. This is because the value-based approach leverages immediate feedback and doesn't require sampling entire trajectories. On the other hand, the policy-based method (e.g., REINFORCE) adjusts action probabilities directly, which allows for more flexible exploration of diverse paths. This characteristic makes it naturally more compatible with deep neural networks. Finally, the learned policies guide the agent as follows:


Value-Based(Q-Learning) and Policy-Based (REINFORCE) learned policies - CSY
Conclusion
In RL, value-based and policy-based methods offer distinct approaches to solving problems like navigating a 3x3 grid maze. Policy-based methods (e.g., REINFORCE, TRPO, PPO, GPO) directly learn a probabilistic policy, enabling flexible, exploratory behavior ideal for continuous action spaces or stochastic environments, but they can be sample-inefficient due to high variance.
Value-based methods (e.g., Q-Learning, DQN, Dyna-Q) learn a value function to select actions that maximize expected rewards, offering sample efficiency and stability in discrete action spaces, but they rely on explicit exploration and struggle with continuous actions.
Hybrid methods like actor-critic combine their strengths for robust performance. Choose policy-based for flexibility, value-based for efficiency, or hybrids for complex task.
"What I cannot create, I do not understand." — Richard P. Feynman



